[This article was originally published by wonkHE.]
It is good to see equality measurement in higher education is receiving serious attention again. It is important.
But the debate often seeks to establish what measure is “best”. POLAR and MEM were not meant to be this kind of either/or choice. And those responsible for widening participation in universities shouldn’t feel forced to take sides between the two. It can help to go back to basics about what they are designed to do. And what they are not.
What POLAR does
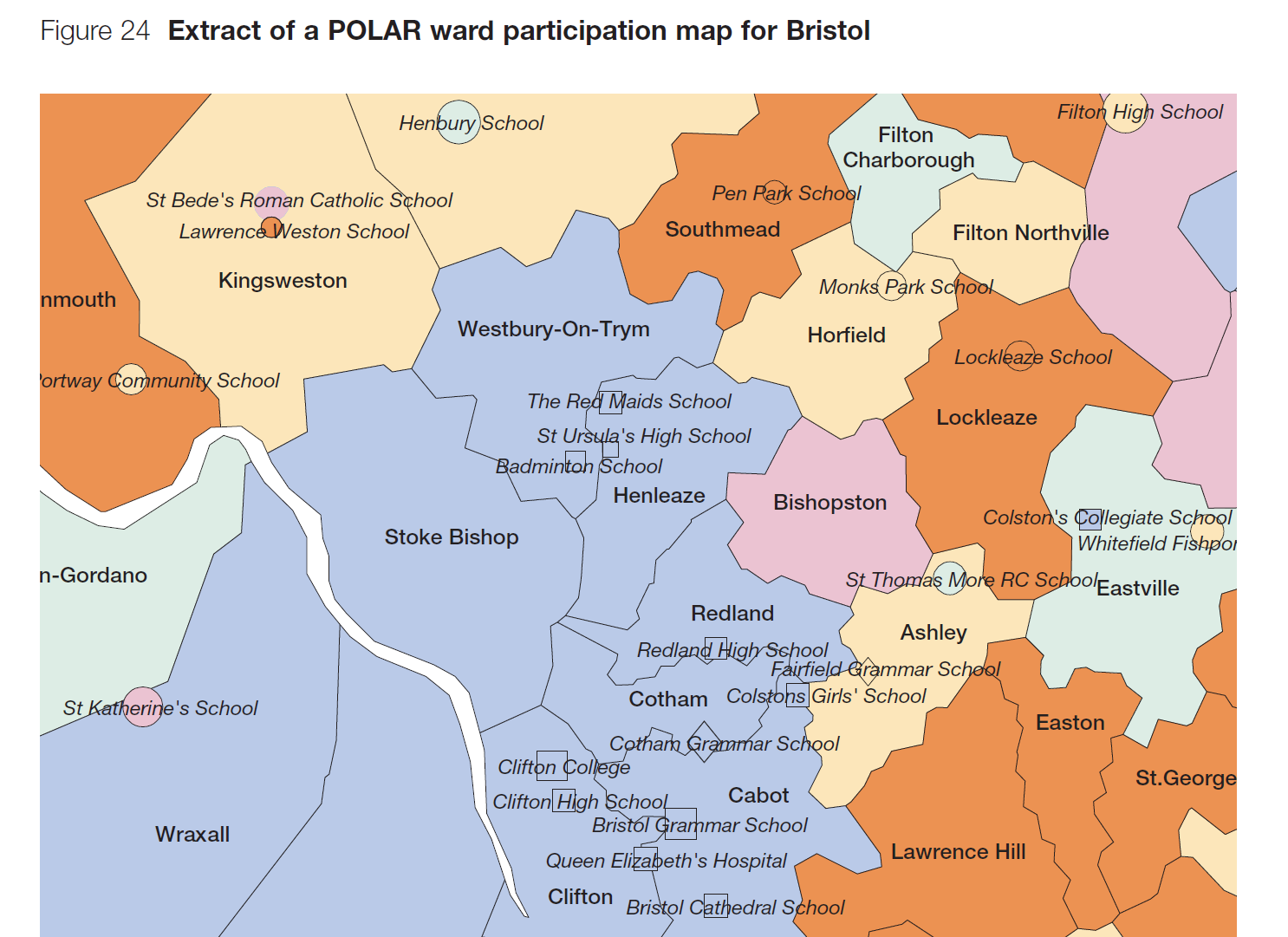
POLAR (Participation Of Local Areas, developed at HEFCE) is simple. It does what it says: assign young people to groups by their observed higher education entry level alone across a high resolution geography of neighbourhoods. It doesn’t presume to have an underlying social model of what causes low higher education entry. Instead it serves a policy agenda which is “we want to tackle low entry to higher education, whatever lies behind it”.
POLAR’s underlying assumption is that people who live in the same neighbourhoods are often more similar to each other than they are to people who live in different neighbourhoods. It is a single-dimensional measure, but has some multi-dimensional characteristics, simply because the forces that form neighbourhoods are. It consistently shows high discrimination across a range of higher education-related statistics, reflecting the strong partitioning of residential neighbourhoods in the UK. And it has a small data footprint, making it usable for both monitoring (we recommend POLAR3 if looking at trends), targeting (POLAR4) and evaluation (either).
There are a large number of things POLAR doesn’t do but people sometimes seem to expect it to. For example, it doesn’t partition people with low household incomes from those with other incomes. If that was your intent it would be much better to form groups by, say, low household income. In terms of higher education equality, you might be forced to use such an income proxy if you couldn’t measure higher education entry directly. But you can measure and target directly by the policy issue you are interested in, low higher education entry. Which is what POLAR does. And does well, within the limitations of being a single-dimension measure. But the multi-dimension nature of inequality in entry to higher education means no one single-dimension measure can properly reflect groups with low entry rates.
How MEM builds on POLAR
Enter the Multiple Equality Measure (MEM), developed by UCAS.
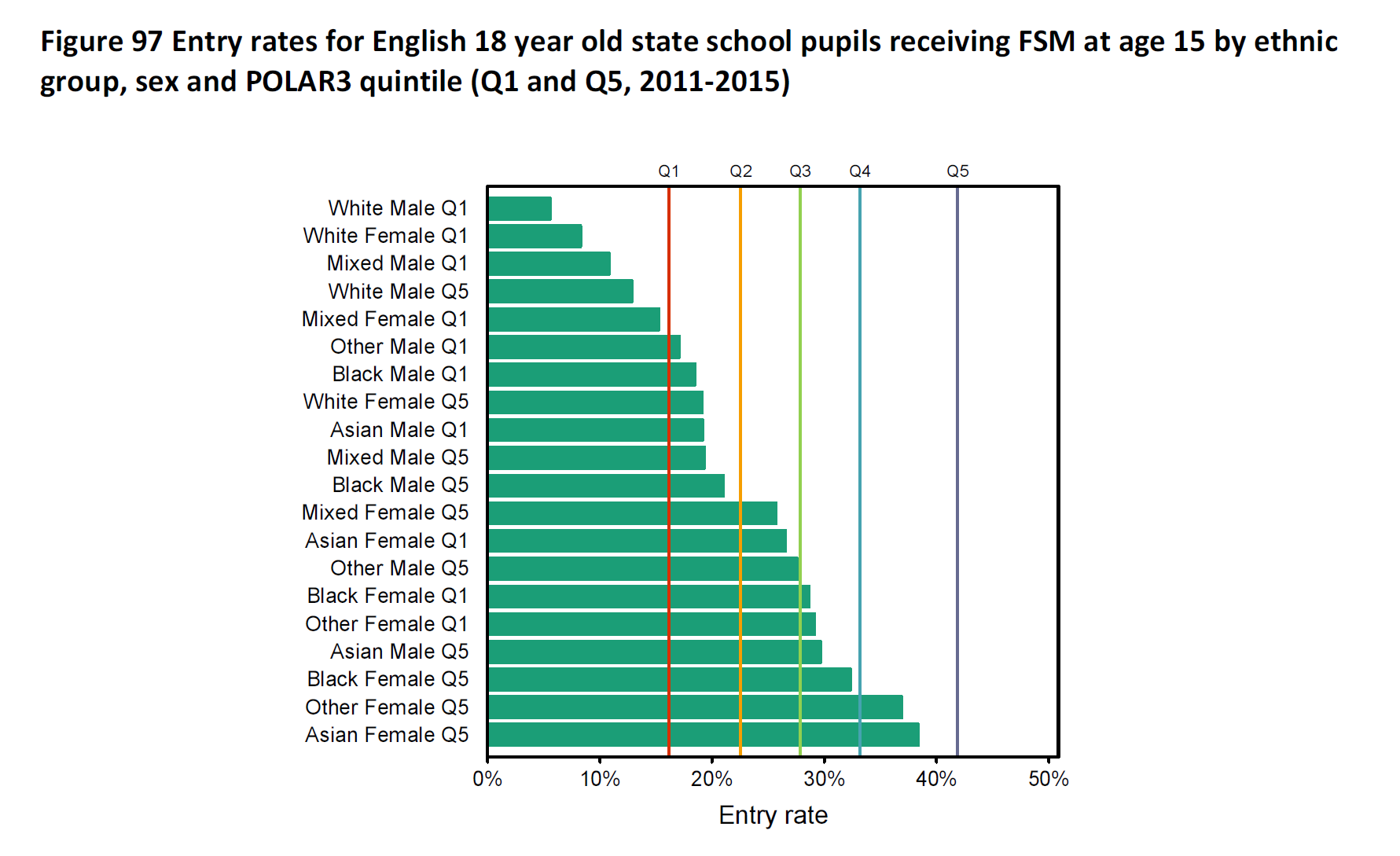
I see MEM as more of a framework than a measure. The motivation for developing it was to be able to bring the strengths of different single-dimension measures together in a data-led way. This is especially important for dimensions that are associated with equality patterning within neighbourhoods (for example, variations in income) and, even more so, within households (sex). I also thought that it could help to reduce the amount of time and energy the sector spends deliberating over which single measure was best: it hasn’t.
MEM’s underlying statistical model predicts higher education entry probability at individual level using only factors that (by agreement) shouldn’t matter to higher education entry rates. These probabilities are then ranked to form quintiles, like POLAR. Indeed POLAR and MEM are closely related. If you build a MEM model using only indicators for each of the neighbourhoods used in POLAR (essentially saying “the neighbourhood where you live shouldn’t matter to your chances of going to university”) MEM is POLAR. The strength of the MEM framework over POLAR is that you can add in a whole set of factors together. You can’t go completely wild here, or you will end up with individuals, but you can go a long way. Then you can make that powerful “shouldn’t matter” statement jointly across all factors, with the resulting statistics showing how distant equality is from this statement.
In this way a correctly formulated MEM is conceptually superior to POLAR. And this is reflected in the greater entry rate differentials between the MEM quintiles. But this comes at the cost of very high (and intrusive) data collection requirements on, for example, outreach activities students if you want to use operationally. And to calculate the rates you would need to have access to that same type of data in the underpinning population estimates too. This is heavy duty data analysis. This makes MEM more suitable for specialised measurement in very data rich settings: more laboratory than in the field, where POLAR is a more practical choice. Comparing the two allows a scaling of the penalty of using POLAR as a practical implementation against a complex multi-dimensional reality.
Comparing POLAR and MEM
We’ve looked at this at dataHE (using the last detailed data UCAS published on MEM, the 2017 version, and neglecting Independent school pupils). This shows that using POLAR Q1/Q2 to identify the (lowest 40 per cent) MEM G1/G2 captures just under three quarters of that ‘true’ population group. Not bad for a field measure. The quarter that POLAR Q1/Q2 misses of MEM G1/G2 are mostly men (around 85 per cent), reflecting the strong gradient of entry rate by sex within households (that POLAR can’t see). The free-school-meals (FSM) group forms around 40 per cent of that missed quarter: a very substantial over-representation but, numerically, there are still more “non-FSM” who are missed than FSM. For the same reasons, FSM alone is poor at capturing that key MEM G1/G2 group.
One drawback with MEM is that the more complicated methodology does give heavy reliance on it being correctly formulated. It is not clear this has been the case since the latest revision at the end of last year. This introduced admission policy within state schools (for example, comprehensive/selective/modern/etc) to the set of factors that “shouldn’t matter”. The problem here is that admissions policy acts as a direct measure of individual prior attainment. And individual prior attainment is generally regarded as a factor that “should matter” to higher education entry in the UK system. With admission policy included the underlying logic of the MEM model, “only factors that shouldn’t matter”, frays. This make the classification currently rather less useful for that perspective than it should be.
Equality measurement and activity targeting are too important not to get right. POLAR is a strong single-dimension measure and widening participation staff can feel confident in using it as such. But they should continue to be alert to other equality dimensions – most clearly sex –where entry can vary within neighbourhoods in a way that POLAR can’t see. The MEM framework handles these variations analytically. It can give a more holistic picture of equality. But it needs lots of data and careful statistical handling, which limits how it can be used. Ultimately MEM is the better laboratory measure, but POLAR is more practical. Both can help universities with equality.
[ You can find the original HEFCE 2005/03 report that set out POLAR at the national archives.
MEM was first described in the 2015 UCAS End of Cycle report on the UCAS website. ]